Glyph Grammar: A System for Procedurally Generating Alphabets

Life Update

Have been pretty good at making a monthly update here on my site the last year or so, but have seemed to miss the month of May. This blog has all less been aimed at getting people to read and look at my work, more about keeping myself accountable with creative activities. However past couple months have been pretty busy with a lot of life and work stuff so haven’t had to time to progress things to make a post here. One thing I started doing IRL though is Improv Comedy over at a local theater called Mettlesome. performing and specifically improvising in front of an audience is something new and very different for me (by the gods, I became an engineer for a reason!) and something I can recommend to anyone looking to improve social skills after the pandemic.

Inspiration

In keeping with thoughts about fantasy world building, I was thinking about how alphabets are created. Was looking at the Phoenician alphabet specifically and was inspired how each glyph could generally be broken down into discrete parts. Yes, technically it is all lines, but beyond that it is just rectangles, triangles, and circles, with some segments removed on occasion.

Phoenician Alphabet - source: Wikipedia

So to create new Phoenician-like alphabets, we’d just need a system to generate, modify, and combine those shapes.

Procedural Glyphs

Early attempts were kind of sketchy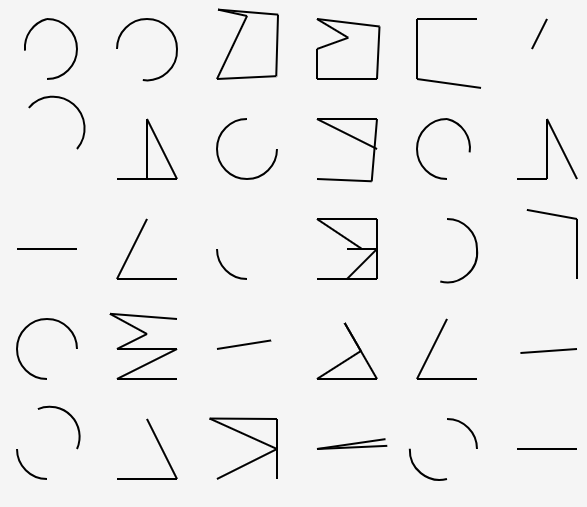

Naive attempts at randomization, while sort of interesting, didn’t approach something that looked like an alphabet.

Some of this was due to bugs in the code, but I didn’t really have an overall way of organizing everything.

Glyph Grammar

Then I remembered L-Systems. Basically a formal grammar for procedurally creating interesting models. I didn’t think L-systems were the answer really for the procedural generation, but an L-system style grammar could be implemented (and eventually we could test out the L-system, although recursive fractals don’t really seem to be the best solution for generating alphabets). However a grammar would be useful for reducing characters down to a string representation which would make use some other interesting analysis.

The grammar I ended up using was:

Primitives:

• C: Circle
• T: Triangle (3 sided polygon)\
• R: Rectangle (4 sided polygon, technically a square)
• S: Starburst, 8 lines by default

Modifiers:

• |: Denote new row
• *: Denote overlapping primitives
• []: Group primitives
• X: where X is a decimal representation of a bitmask indicating which segments of a primitive to show. Ie (R1) (0001 in binary) would show a rectangle with only its first segment showing) R9 (1001 in binary) would show the first and last segments. Triangles are 3 bits (e.g. 101), while starbursts are 8 bits (e.g. 01010101), representing the cardinal and ordinal directions. No number indicates the full primitive is shown.
• rX: Rotation, where X is a decimal representation of the angle to rotate the glyph by. (e.g. Tr90, rotate triangle by 90 degrees)

Phoenician Alphabet

Using this grammar you can encode the entire Phoenician alphabet into a simple JSON:

phoenician_glyphs = {
  "aleph": "T5r270*S17",
  "bet": "Tr270|R6",
  "giml": "T3r270|R2",
  "delat": "T",
  "he": "R3|R3|R3|R3",
  "waw": "S146",
  "tet": "S170*C",
  "zayin": "R5*S17",
  "het": "R12R6|R13R7|R13R7|R9R3",
  "tet": "C*S170",
  "yod": "R3|R3R4",
  "kap": "S177|S1",
  "lamed": "S17|S3",
  "mem": "T5r180 T5r180 R8 | R0 R0 R8 | R0 R0 R8",
  "nun": "T5r180 R8 | R0 R8 | R0 R8",
  "samekh" : "R3R9|R3R9|R3R9|R3R9",
  "ayin": "C",
  "pe": "C3",
  "sade": "S19S130",
  "qop": "[C*S17]|S1",
  "res": "Tr270|R2",
  "shin": "T5r180T5r180",
  "taw": "S170"
}

Which when combined with a grammar parser produces the following image:

Pretty accurate, main remaining issues are the ‘sade’ and ‘pe’ glyphs which aren’t completely accurate to the originals. This begs a few additions to the grammar:

• t: transpose a glyph, so that not everything has to perfectly fit the grid system
• s: scale a glyph
• c: curve a line segment, potentially with some simple parameter for the bezier curve
• starbursts work off of a consistent radius. we need an option for a starburst with lines effectively reaching the bounds of the box, rather than a circular radius

Implementing the above would get this to 1.0 and also let us fully implement the Runic alphabet. Although we could implement most of those glyphs right now as well.

Runic Alphabet - source: Wikipedia

Technically with the above we could also implement Chinese characters too. When doing research for the above I found there’s a project that sort of does that already in a cool way too

Procedural Generation

We got this far without getting to the main point: actually procedurally generating new alphabets. We had too much fun with the grammar and ran out of time (i wanted to make a post of something for this month). We could try an actual L system, while I don’t think that would be what we want it would at least be interesting to see the results. Rather we should do some analysis and base our procedural rules on the alphabets we already have available, sample the ratios and combinations that come and repeat them. And also do something for symmetrey. We’ll get to that next.

Working Demo

As an aside I used JS Fiddle for this but I think I won’t again. The IDE doesn’t work well on Firefox and at one point bugged out, costing me some unsaved work that I had to do. But it is what I used so far. Please forgive the code, right now it is basically a messy sketchbook, not a finished piece lol.

Tweet Share